The simple projection of an unknot is just a circle.

How do we prove that there exist knots for which the unknot is not a projection (i.e. cannot be arrived at through a Reidemeister move)?

For this proof we introduce the concept of tricolorability. Let a strand be defined as that portion of a knot that begins at an undercrossing and ends at the next undercrossing, such that the only crossings in between the strand’s endpoints are overcrossings. The following image shows the the trefoil knot’s three strands:

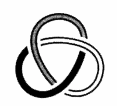
For a knot to be tricolorable, it must be the case that each strand can be assigned one of three distinct colors such that at each crossing, either 1) strands of three different colors join, or 2) strands of a single color join. A tricolorable knot must utilize at least two colors. Clearly in the image above, the trefoil knot is tricolorable.

Tricolorability turns out to be a binary invariant for projections of a knot.

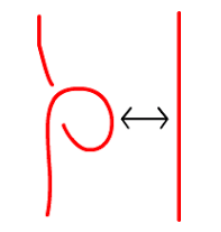
Consider Reidemaster move 1: twisting a knot (i.e. adding one crossing). After introducing a knot, color all involved strands the same color to preserve tricolorability. Conversely, an existing twist involves only two strands, so in an already-tricolorable knot, this twist must have only contained one color.

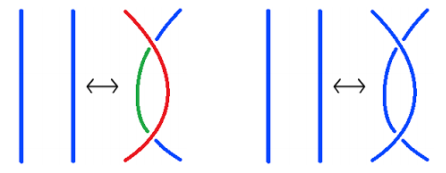
Reidemaster move 2: introducing two crossings. If the two prior strands were the same color, keeping the same color scheme after Reidemaster move 2 preserves tricolorability. If they are of different colors, the newly created strand between the two new crossings can be assigned a third color to preserve tricolorability.

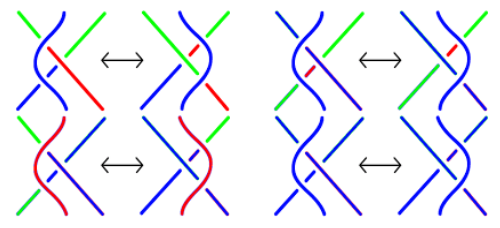
Reidemaster move 3: sliding a strand over a knot. In each of four cases demonstrated below, a color scheme exists to preserve tricolorability.

The unknot cannot be tricolorable because it does not have strands and therefore cannot be of greater than two colors. Because tricolorability is preserved under Reidemaster moves, it must be the case that all projections of a given knot must all be tricolorable, or none at all. Any tricolorable knot therefore cannot contain the unknot as a valid projection.